几何课堂如何告别“死记定理、机械解题”的困境，真正唤醒学生的逻辑思维？这本2000多年前的数学经典——《几何原本》，给出了最具深度的答案！

　　《几何原本》是古希腊数学家欧几里得编纂的数学巨著。其革命性意义在于建立了人类历史上第一个完整的公理演绎体系。它以5条公理、5条公设为坚实起点，用环环相扣的严密逻辑，将万千图形、定理串联成系统化的思维殿堂，堪称“逻辑推理的教科书”。

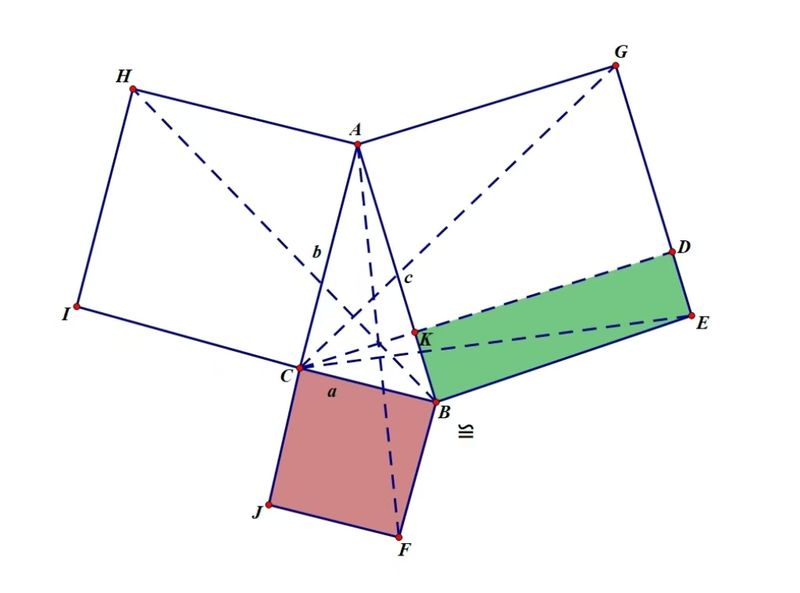
　　《几何原本》全书共13卷，前6卷系统阐述了平面几何的基本理论，包括三角形的性质、平行线公理、勾股定理以及相似图形。书中对勾股定理第1卷命题47的证明完美体现了欧几里得的逻辑艺术。他并未使用代数计算，而是通过精妙的几何构造来揭示面积关系：在直角三角形各边上作正方形后，通过从直角顶点向斜边作垂线，将斜边上的正方形分割为两个矩形；然后证明每个直角边上的正方形面积恰好等于斜边上对应的矩形面积。这个证明过程就像一场几何魔术，通过证明几对三角形的全等关系，最终展现出两个小正方形面积之和等于大正方形面积的必然结论，其推理之精巧令人叹为观止。7-9卷将几何方法应用于数论领域，深入探讨了比例理论、质数性质，并给出了著名的欧几里得算法。第10卷专注于无理量的分类与研究，11-13卷则拓展到立体几何，完整研究了棱锥圆柱、球体等立体图形的性质。

　　在几何教学中，它能引导师生跳出“记公式、套题型”的惯性误区，跟着欧几里得的思路追溯每一个结论的本源：为什么三角形内角和必然是180°？为什么全等三角形的判定定理绝非偶然？在“公理—定义—命题—证明”的层层推演中，学生不仅能扎实掌握几何知识，更能习得“从本源到结论”的逻辑思维方式，读懂数学的严谨性与内在美感。

　　当课堂不再是定理的单向灌输，而是让学生亲历“观察—猜想—推理—验证”的完整过程，几何便从枯燥的公式列表，变成了充满探索乐趣的思维之旅。学生将明白，数学的核心不是“记住答案”，而是“如何找到答案”，这种思维能力终将迁移到各类问题解决中，使他们受益终身。

　　无论你是深耕教学的教师，还是渴望探索真理的学生，《几何原本》都值得纳入你的书单，它不仅是数学殿堂的经典基石，更是能帮你筑牢理性思维、涵养科学精神的思想指南。若你也想亲身感受逻辑推理的魅力，体验数学的严谨之美，不妨翻开书页，和我们一同探锁数学世界的无穷奥秘。

　　撰稿：马慧芳

　　编辑：潘舒璠

　　审核：魏艳红